Proteins make waves and surf them in the cell membrane

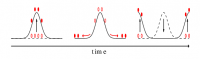
A new stochastic equation for active, growing interfaces predicts the evolving shape of a cellular membrane.

From a physicist's point of view, perhaps the most intriguing feature of biological systems is that they are constantly held away from thermodynamic equilibrium by active processes: the inert atoms and molecules of classical statistical mechanics are replaced by active entities which consume energy and may move of their own volition. Likewise active matter - which is composed of many such active entities - can itself grow and change shape.

The range of lengthscales spanned by theories of active matter is stunningly large. Consider a cell: on the one hand it is the active component of bigger systems such as tissues, on the other hand it is itself an active system, whose constituents are those proteins regulating the whole cellular machinery.

Francesco Cagnetta (Higgs STFC PhD student), Martin Evans (Professor of Statistical Physics) and Davide Marenduzzo (Professor of Computational Biophysics) analyse the effects of activity on growing interfaces and how this produces the striking patterns that have been puzzling experimentalists studying red blood cell membranes.  Specifically, the authors extend the celebrated Kardar-Parisi-Zhang (KPZ) equation, known to predict the universal features of many out-of-equilibrium systems, to deal with the local source of growth provided by membrane proteins.  Their theory proposes an explanation for the self-organisation of proteins: dynamic nanoclusters of proteins are formed which induce travelling waves of growth in the membrane. Intriguingly, these travelling undulations of the membrane are in turn surfed by the protein nanoclusters that produced them!

The work was made an Editors' Selection in Physical Review Letters and has been highlighted by a Viewpoint in APS Physics.