Statistical Physics and Complexity

Statistical physics sets out to explain how the patterns and structures around us in the macroscopic world arise from the interactions between their component parts. A major challenge in the 21st century is to extend statistical physics to systems that are far from equilibrium.

Overview

Statistical physics considers how many microscopic entities (be they atoms, molecules, bacteria, vehicles .....)  may produce macroscopic phenomena. The central challenge of statistical physics in the twenty-first century is to describe nonequilibrium systems where the traditional assumptions of thermal equilibrium and the thermodynamic limit may no longer hold. Compared to equilibrium systems, one is still very much in the dark about nonequilibrium systems. Yet nonequilibrium systems are all-pervasive in nature: complex or biophysical systems require the approaches of nonequilibrium statistical mechanics as do the states of open quantum systems. Here in Edinburgh we conduct a wide programme of fundamental work on model systems which addresses the many novel principles of non-equilibrium physics. Our work also has direct relevance to a wide range of other disciplines, for example, biology, ecology and linguistics.

Statistical mechanics is a major theoretical tool-set that we use for the understanding of complex systems. The systems in question include many non-traditional areas such as ecosystem dynamics and the jamming of traffic, although we also work on more traditional condensed matter.  Modern nonequilibrium statistical mechanics requires generalisations of the traditional thermodynamic concepts such as free energy to notions such as large deviation functions.  Indeed models of nonequilibrium systems are often defined purely in terms of stochastic dynamics rather than any thermodynamic concepts and consequently their study requires the development of novel dynamical simulation and theoretical techniques. 

We have strong links with many of the other research themes within the Institute for Condensed Matter and Complex Systems, in particular, Physics of Living Matter, Soft Matter Physics and Computational Materials Physics.

Research interests

Below are some examples of our current research:

Fundamental nonequilibrium systems and phase transitions 

Nonequilibrium systems may generally defined by stochastic dynamics of the microscopic constitutents.  A special case is when the dynamics obey detailed balance, then after a sufficient time the system will relax to an equilibrium state described by the Boltzmann distribution. However, generally stochastic dynamics do not obey detailed balance and the system will relax to a nonequilibrium stationary state in which currents are present. We are just beginning to discover the nature and potential of such states.

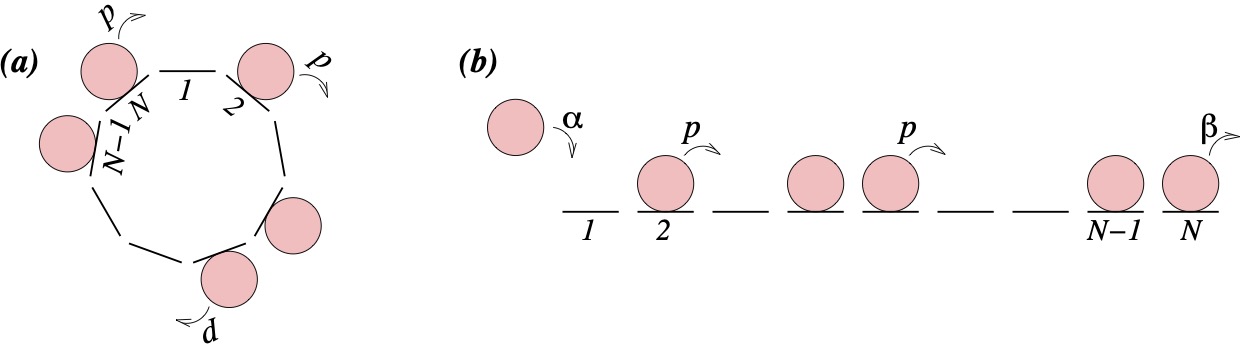
By studying and solving simple mathematical models we can elucidate the properties nonequilibrium states.  For example a simple lattice gas known as the 'asymmetric exclusion process' is illustrated in the figure above. Particles move stochastically along a lattice but cannot overtake each other. When particles are injected at one end and removed at the other a nonequilibrium stationary state is attained. This system is a basis for modelling general transport problems including vehicular traffic and biophysical traffic such as ribosomes (large complex molecules) proceeding along and translating RNA.

Remarkably it has been shown that nonequilibrium phase transitions occur in this system. That is by varying the boundary injection and extraction rates, dramatic changes in the bulk behaviour of the system occur.

Another nonequilibrium phase transition discovered here in Edinburgh is the real-space condensation transition in which many microscopic constituents coalesce at a single location. It has become apparent that condensation occurs in a wide range of surprising contexts, for example, coalescence in granular gases, jamming in vehicular flows, hub-formation in networks and wealth condensation in macroeconomics – where a single agent garners a finite faction of the wealth in the system! The phenomenon is related to the quantum Bose-Einstein condensation. A theme of our work has been to elucidate unexpected aspects of this phenomenon such as the curious dynamics of moving condensates. 

Statistical physics of evolutionary dynamics

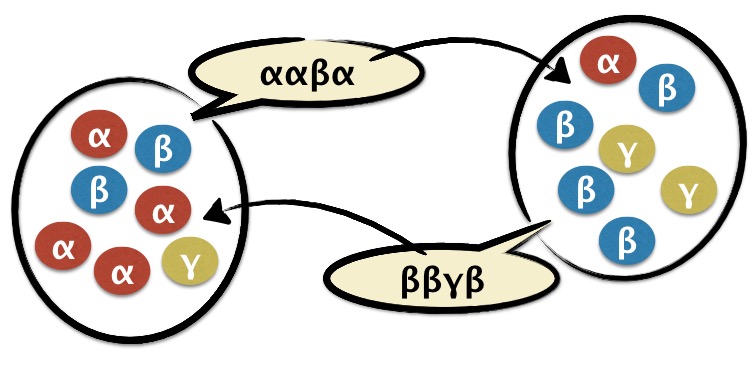
Evolution is a theory of change by replication (copying), and arises in both biology, where DNA molecules and more complex organisms are replicated, and culture, where learned behaviour is passed on between agents by learning (as shown in the figure). This replication process is inherently random – the timing and nature of replication events is unpredictable. Moreover, the dynamics do not possess the time-reversal symmetry that underpins physical systems at equilibrium. Therefore, evolving populations constitute a class of nonequilibrium dynamical systems that are of great interest from a statistical physics viewpoint.

In particular, the nonequilibrium nature of the fluctuations in replication dynamics leads to a variety curious macroscopic effects that we are yet to fully work out.  For example, whilst weak fluctuations can destroy cyclic behaviour that is present in a deterministic system, we have found that the fluctuations that are endemic in evolving populations can have the opposite effect, that is, introduce cycles into a system whose deterministic limit only has stable fixed points. At the same time there are applications of these models to a variety of real-world phenomena, particularly in the dynamics of language where we have examined the formation of the New Zealand English Language dialect and how children learn the meanings of words.

Statistical-physics models of biological populations

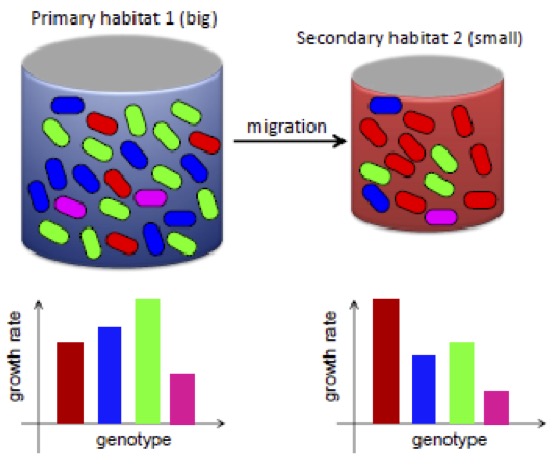
Statistical physics finds many applications in modelling dynamics and evolution of biological populations. As these systems are out-of-equilibrium due to replication and growth of organisms, phase transitions can occur even in zero- or one-dimensional systems.

Examples range from extraction of membrane tubes by molecular motors, to bacterial "colloids" sedimenting under the force of gravity, to models of migrating organisms. The mathematical framework used to model these systems is very similar to that used to address other phenomena in statistical and condensed matter physics: condensation, localization, and jamming, as well as many problems that occur in modelling chemical reactions such as travelling waves. 

Statistical-physics models of biological cells

Inside biological cells, a multitude of biochemical reactions happen. These allow the cell to capture energy from food, make new cell components and react to stresses like changes in temperature or influx of a drug. Using techniques from statistical physics, we can make models for these processes. For example, we use advanced computer simulation techniques to predict how DNA is arranged inside biological cells. We also develop network-based algorithms for investigating the optimality of biochemical pathways for energy metabolism, and we construct simple dynamical models for the response of bacterial cells to antibiotics.

Networks and Agents in Physics and Ecology

This work addresses the evolution of interacting objects under nonequilibrium conditions. The objects are often not merely passive but dynamic 'agents' which act according to some evolvable strategy: moreover, interaction between agents determines their response to, and effect on, their environment. Evolution is defined in terms of evolutionary game theory in which the survival and replication of the objects is determined by their success in achieving a particular aim. This may be avoiding a predator, selling a product or converting to a particular culture.  From a computational viewpoint, this means that the numerical value of many parameters which have a complicated interpretation can be determined by the evolutionary process rather than by data fitting.

These individual-based models can show behaviour much richer than the equivalent continuum theories to which they reduce in the large number long-term limit. Possible projects which could be addressed using this methodology include understanding boom and bust economics, drivers for development of flocks and cities, and understanding the rise and fall of civilizations.

The figure shows results from a simulation of the spread of neolithic farming, which is based on the techniques described above. Top panels show demic spread, from the genetic descendents of the original middle eastern farmers, lower panel shows spread by adopters of the farming technology. 

PhD project opportunities in Statistical Physics and Complexity

People in Statistical Physics and Complexity

Telephone numbers in the list below are shown as UK numbers. Callers from outside the UK should remove the leading zero and use the UK country code (+44).

Name	Position	Contact details	Location	Photo
Academic staff
Graeme Ackland	Professor	gjackland [at] ed.ac.uk 0131 650 5299	JCMB 2502
Richard Blythe	Professor	r.a.blythe [at] ed.ac.uk 0131 650 5105	JCMB 2505
Chris Brackley	Lecturer in Theoretical/Computational Condensed Matter Physics	C.Brackley [at] ed.ac.uk 0131 650 5881	JCMB 2612
Jean-Christophe Denis	Lecturer	j.c.denis [at] ed.ac.uk 0131 650 5263	JCMB 2603
Martin Evans	Professor of Statistical Physics	m.evans [at] ed.ac.uk 0131 650 5294	JCMB 2615
Davide Marenduzzo	Personal Chair in Computational Biophysics	Davide.Marenduzzo [at] ed.ac.uk 0131 650 5289	JCMB 2506
Patrick Pietzonka	Lecturer in Theoretical Soft Matter, Statistical and Biological Physics	p.pietzonka [at] ed.ac.uk 0131 650 7181	JCMB 1614
Elton Santos	Reader in Theoretical/Computational Condensed Matter Physics	esantos [at] ed.ac.uk 0131 651 7688	JCMB 2503
Tyler Shendruk	Reader in Theoretical/Computational Condensed Matter Physics	t.shendruk [at] ed.ac.uk	JCMB 2422
Bartlomiej Waclaw	Reader	bwaclaw [at] ed.ac.uk 0131 651 7688	JCMB 1614
Research staff
Davide Michieletto	Royal Society Research Fellow	davide.michieletto [at] ed.ac.uk 0131 651 7742	JCMB 1505
Peter Mottishaw	Visitor	peter.mottishaw [at] ed.ac.uk 0131 650 5881	JCMB 1602
Research postgraduates
Robin Burton	Postgraduate Student	robin.burton [at] ed.ac.uk	JCMB 2510
Auro Varat Patnaik	PhD Student	auro.patnaik [at] ed.ac.uk	JCMB 1511